[Course on SLAM] Chapter 4 / Graph-based SLAM

 

수식이 틀어지는 경우, 수식에 우클릭을 하고 math setting -> math renderer -> SVG를 선택 후 새로고침 바랍니다 : )

Graph-based SLAM

4.1 Problem formulation

아래 사진은 모바일 로봇이 미지의 환경을 돌아다니며 자신의 이동을 추정하고 물체를 탐지하는 SLAM에서의 한 상황이다.

Fig 1.1

그렇게 만든 지도는 로봇 자신이 어디있는지 아는 데 사용된다.

이를 graph 로 구성된 관계로 그려보면 다음과 같다.

Fig 4.1

이 그림은 실제 로보틱스에서 localization과 mapping 문제를 잘 나타낸다.

왼쪽은 물체의 상대적인 위치와 방향을 그려놓은 것이다.

오른쪽은 왼쪽과 같은 상황에 대해서 edge와 node인 그래프로 표현한 것이다.

파란색인 edge는 motion에 대한 측정값을 나타낸다.

빨간색은 물체의 측정값을 나타낸다.

4.1.1 SLAM as a Dynamic Bayes Network

과정은 dynamic Bayes network(DBN)으로 잘 나타낼 수 있다.

DBN은 확률론적 그래픽 모델(통계모델의 일종)이다.

DBN은 확률론적 방향 비순환 그래프를 통해 랜덤 변수 집합과 그들의 조건부 의존성을 나타낸다.

조건부 의존성은 방향을 가진 화살표로 두 개의 변수를 연결한다.

그래프에서 $A\leftarrow B$는 "$A$가 $B$에 의해 조건이 붙는다." 혹은 "$A$가 $B$에 의존한다."라는 것을 의미한다.

비순환적인 속성은 '$A$가 $B$에 종속되고 B가 C에 종속되고 C가 A에 종속되는' 유형의 종속성 루프를 발생시키지 않음을 보장한다.

우리의 경우 네 가지의 랜덤 변수가 존재한다.

• 모든 로봇의 state, $X={\mathbf{\text{x}}}_i$, $i\in 0\cdot \cdot \cdot M$.
• 모든 랜드마크의 state, $L={\mathbf{\text{l}}}_j$, $j\in 1\cdot \cdot \cdot N$.
• 모든 로봇의 controls, $U={\mathbf{\text{u}}}_j$, $i\in 1\cdot \cdot \cdot M$.
• 모든 랜드마크의 measurements, $Z={\mathbf{\text{z}}}_k$, $k\in 1\cdot \cdot \cdot K$.

섹션 2.3에서 나온 것처럼 로봇의 motion controls 때문에 시간 $t=i$에서의 pose ${\mathbf{\text{x}}}_i$는 $t=i-1$에서의 pose와 시간 $t=i$에서의 control ${\mathbf{\text{u}}}_i$에 의존한다.

이 motion model을 다음과 같이 쓸 수 있다.

$${\mathbf{\text{x}}}_i=f_i({\mathbf{\text{x}}}_{i-1},{\mathbf{\text{u}}}_i)+{\mathbf{\text{w}}}_i\cdots \cdots (4.1)$$

그리고 이것은 ${\mathbf{\text{x}}}_{i-1}$과 ${\mathbf{\text{u}}}_i$가 주어졌을 때 ${\mathbf{\text{x}}}_i$의 조건부 확률을 나타내는 서브 그래프로 다음과 같이 나타낼 수 있다.

식 4.2

$$P({\mathbf{\text{x}}}_i|{\mathbf{\text{x}}}_{i-1},{\mathbf{\text{u}}}_i).\cdots \cdots (4.2)$$

 

비슷하게, 환경에 대한 각각의 측정값도 아래와 같이 모델링 될 수 있다.

$${\mathbf{\text{z}}}_k=h_k({\mathbf{\text{x}}}_i,\mathbf{\text{m}})+{\mathbf{\text{v}}}_k\cdots \cdots (4.3)$$

이것은 환경에 대한 맵 $m$에 의존하며 측정된 당시의 pose는 ${\mathbf{\text{x}}}_i$이고 서브 그래프로 다음과 같이 나타낼 수 있다.

식 4.4

$$P({\mathbf{\text{z}}}_k|{\mathbf{\text{x}}}_i,\mathbf{\text{m}}).\cdots \cdots (4.4)$$

서브 그래프를 합하면 Fig 4.2의 왼쪽에 해당하는 DBN이 나온다.

Fig 4.2

물론 여기서 m은 환경 지도를 나타내는 추상적인 엔티티로, SLAM 프레임워크의 설계에 따라 여러 형태를 취할 수 있다.

흥미로운 부분은 지도가 개별적으로 측정 가능한 랜드마크로 바뀌었을 경우이다.

이런 경우에는 pose ${\mathbf{\text{x}}}_i$로부터의 랜드마크의 측정값 $l_j$는 다음과 같이 모델링 될 수 있다.

$${\mathbf{\text{z}}}_k=h_k({\mathbf{\text{x}}}_i,{\mathbf{\text{l}}}_j)+{\mathbf{\text{v}}}_k\cdots \cdots (4.5)$$

서브그래프 표현은 다음과 같다.

식 4.6

$$P({\mathbf{\text{z}}}_k|{\mathbf{\text{x}}}_i,{\mathbf{\text{l}}}_j)\cdots \cdots (4.6)$$

식 4.2에 나온 서브그래프와 식 4.6의 서브그래프를 합하면 Fig 4.2의 오른쪽에 나오는 DBN이 도출된다.

이것은 Fig 1.1에서 나온 상황을 정확히 보여준다.

그림을 보면 각각의 랜드마크가 명확히 보인다.

일반성을 잃지 않고, 랜드마크가 있는 경우에 중점을 둬보자.

 

이렇게 구성된 DBN은 문제의 모든 변수 간의 모든 종속성을 포함한다.

그것은 그래프에 표시되지 않은 모든 것이 독립적이며 따라서, trajectory, map, controls, measurements의 결합 확률들이 다음과 같이 조건부 곱으로 표현될 수 있음을 의미한다.

$$P(X,L,U,Z)\propto P({\mathbf{\text{x}}}_0)\prod _{i=1}^{M}P({\mathbf{\text{x}}}_i|{\mathbf{\text{x}}}_{i-1},{\mathbf{\text{u}}}_i)\prod _{k=1}^{K}P({\mathbf{\text{z}}}_k|{\mathbf{\text{x}}}_{i_k},{\mathbf{\text{l}}}_{j_k})\cdots \cdots (4.7)$$

$P({\mathbf{\text{x}}}_0)$은 초기 로봇 자세에 적용된 prior을 나타낸다.

마지막으로, SLAM estimator의 목적은 저 확률을 최대화하는 변수인 $X^{\ast },L^{\ast }$을 찾는 것이다.

아래와 같이 나타낼 수 있다.

$$X^{\ast },L^{\ast }=\underset{X,L}{\mathrm{argmax}}P({\mathbf{\text{x}}}_0)\prod _{i=1}^{M}P({\mathbf{\text{x}}}_i|{\mathbf{\text{x}}}_{i-1},{\mathbf{\text{u}}}_i)\prod _{k=1}^{K}P({\mathbf{\text{z}}}_k|{\mathbf{\text{x}}}_{i_k},{\mathbf{\text{l}}}_{j_k})\cdots \cdots (4.8)$$

4.1.2 SLAM as a factor graph

식 4.7의 결합 확률(A와 B가 동시에 발생할 확률)은 4.2와 4.6의 M+K개의 요소의 곱으로 나타낼 수 있으며, 이들은 모두 독립적이다.

이러한 요소들은 각각 적은 수의 state 노드에 의존하는 측정에서 비롯된다.(pose 또는 landmark 혹은 두 개 다 섞인)

따라서 이 그래프를 그러한 요소들을 명시적으로 나타내는 그래프로 변환하는 것이 좋다.

이를 factor graph라고 하며 Fig 4.3을 참고하자.

Fig4.3 랜드마크 기반 SLAM의 factor graph를 나타낸다. 왼쪽 그래프 : 알려진 데이터를 나타내는 노드는 알려지지 않은 변수 또는 state(원)에 연결된 factor(네모)로 대체되었다. 오른쪽 그래프 : 모든 state(pose와 landmark)가 동일하게 레이블이 지정되어 있는 동일한 그래프이며, 고유한 인덱스 $i\in 0,\cdot \cdot \cdot ,7$로 표시되며, 모든 factor(controls, measurements)도 동일하게 인덱스 $k\in 1,\cdot \cdot \cdot ,10$으로 표시되어 있다.

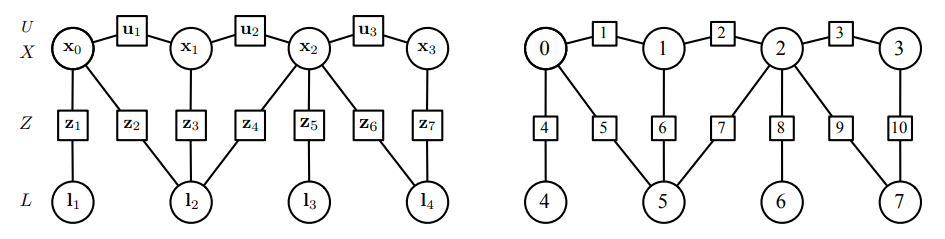
Factor graph는 두 종류의 노드를 가지고 있는 이분 그래프이다.

Variable node들은 로봇의 state를 구성하고 factor node들은 state들 사이에 제약 조건을 구성한다.

인자들은 시스템에 들어오는 모든 정보를 부호화하고 그래프는 이 정보가 우리가 추정하려는 숨겨진 상태로 전달되는 방식을 포착한다.

Factor를 구성하는 조건부 확률(4.2-4.6)은 모션과 측정 모델에 의해 쉽게 알아낼 수 있다.

motion model과 measurement model이 생소하다면 챕터 2와 3을 다시 보는 것을 추천한다.

그 모델들은 다음과 같이 생겼다.

• Robot motion, $\textbf{x}_{i} = f_{i}(\textbf{x}_{i-1},\textbf{u}_{i}) + \textbf{w}_{i},  \textbf{w}_{i} \sim \mathcal{N}$$\left\{\begin{array}{c}0,{\mathrm{\Omega }}_i^{-1}\end{array}\right\}$$ ,$
• Landmark measurements, $\textbf{z}_{k} = h_{k}(\textbf{x}_{i_{k}},\textbf{l}_{j_{k}}) + \textbf{v}_{k},  \textbf{v}_{k} \sim \mathcal{N}$$\left\{\begin{array}{c}0,{\mathrm{\Omega }}_k^{-1}\end{array}\right\}$$ .$

모델 내의 noise ${\mathbf{\text{w}}}_i$와 ${\mathbf{\text{v}}}_k$를 각각의 공분산 ${\mathrm{\Omega }}_i^{-1}$과 ${\mathrm{\Omega }}_k^{-1}$를 갖는 가우시간 변수로 고려함으로써, (즉, 행렬 $\mathrm{\Omega }$는 관측 데이터의 정보 행렬이다.) 우리는 factor들을 $\varphi$로 나타낼 수 있다.

$${\varphi }_i=P({\mathbf{\text{x}}}_i|{\mathbf{\text{x}}}_{i-1},{\mathbf{\text{u}}}_i)\propto exp(-\frac{1}{2}({\mathbf{\text{x}}}_i-f_i({\mathbf{\text{x}}}_{i-1},{\mathbf{\text{u}}}_i){)}^{\mathrm{\top }}{\mathrm{\Omega }}_i({\mathbf{\text{x}}}_i-f_i({\mathbf{\text{x}}}_{i-1},u_i)))\cdots \cdots (4.9)$$

$${\varphi }_k=P({\mathbf{\text{z}}}_k|{\mathbf{\text{x}}}_{i_k},{\mathbf{\text{l}}}_{j_k})\propto exp(-\frac{1}{2}({\mathbf{\text{z}}}_k-h_k({\mathbf{\text{x}}}_{i_k},{\mathbf{\text{l}}}_{j_k}){)}^{\mathrm{\top }}{\mathrm{\Omega }}_k({\mathbf{\text{z}}}_k-h_k({\mathbf{\text{x}}}_{i_k},l_{j_k})))\cdots \cdots (4.10)$$

만약 우리가 고유한 인덱스 k로 오차 값을 ${\mathbf{\text{e}}}_k$로 정의한다면

• Robot motion, ${\mathbf{\text{e}}}_k({\mathbf{\text{x}}}_{i_k-1},{\mathbf{\text{x}}}_{i_k})=f_{i_k}({\mathbf{\text{x}}}_{i_k-1},{\mathbf{\text{u}}}_{i_k})-{\mathbf{\text{x}}}_{i_k},$
• Landmark measurements, ${\mathbf{\text{e}}}_k({\mathbf{\text{x}}}_{i_k},{\mathbf{\text{l}}}_{j_k})=h_k({\mathbf{\text{x}}}_{i_k},{\mathbf{\text{l}}}_{j_k})-{\mathbf{\text{z}}}_k,$

 (4.9)와 (4.10)의 factor들은 고유한 형태를 취한다.

$${\varphi }_k=exp(-\frac{1}{2}{\mathbf{\text{e}}}_k^{\mathrm{\top }}{\mathrm{\Omega }}_k{\mathbf{\text{e}}}_k).\cdots \cdots (4.11)$$

이는 $k$번째 측정에서 오차 ${\mathbf{\text{e}}}_k$를 계산할 수 있다면, 관련된 상태 $i_k$와 $j_k$와 상관없이 계속해서 가능하다는 것을 시사한다.

$${\mathbf{\text{e}}}_k({\mathbf{\text{i}}}_k,{\mathbf{\text{j}}}_k,{\mathbf{\text{z}}}_k),\cdots \cdots (4.12)$$

우리가 motion과 measurement factor 간에 만든 구별은 그리 중요하지 않다.

그러므로 간소화와 더 큰 일반성을 위해, 이후에는 두 가지 유형의 변수만을 고려한다.

1. state to estimate
2. observed data

한편으로는, 우리가 추정하고자 하는 states {$X,L$}이 있으며, 이는 $N$개의 블록으로 구성된 단일 상태 벡터 $\mathbf{\text{x}}$에 수집된다.

여기에서 ${\mathbf{\text{x}}}_i$는 로봇의 state나 랜드마크의 state일 수 있다.

$$\mathbf{\text{x}}={\left[\begin{array}{ccc}{\mathbf{\text{x}}}_1& \cdots & {\mathbf{\text{x}}}_N\end{array}\right]}^{\mathrm{\top }},\cdots \cdots (4.13)$$

반면에, 이러한 상태를 연결하면 control과 measurements를 포함하는 $K$개의 블록으로 구성된 {$U,Z$}의 관측 데이터를 구성할 수 있다.

$$\mathbf{\text{z}}={\left[\begin{array}{ccc}{\mathbf{\text{z}}}_1& \cdots & {\mathbf{\text{z}}}_K\end{array}\right]}^{\mathrm{\top }},\cdots \cdots (4.14)$$

그러면 각 관측 데이터 ${\mathbf{\text{e}}}_k$에 대해서 오차 ${\mathbf{\text{e}}}_k$와 factor ${\varphi }_k$를 계산할 수 있다.

결합확률 (4.7)은 모든 factor의 곱으로 나타낼 수 있다.

$$P(\mathbf{\text{x}},\mathbf{\text{z}})\propto \prod _{k=1}^K{\varphi }_k\propto \prod _{k=1}^{K}exp(-0.5{\mathbf{\text{e}}}_k^{\mathrm{\top }}{\mathrm{\Omega }}_k{\mathbf{\text{e}}}_k)\cdot \cdot (4.15)$$

PDF(확률 밀도 함수)를 최대화하는 것은 이것의 log-likelihood를 최소화하는 것과 동일하며 이는 cost라고 불린다.

이를 정리하면,

$$\mathbf{\text{F}}(\mathbf{\text{x}})\triangleq -logP(\mathbf{\text{x}},\mathbf{\text{z}})=\sum _{k=1}^K{F}_k=\sum _{k=1}^K{\mathbf{\text{e}}}_k({\mathbf{\text{x}}}_i,{\mathbf{\text{x}}}_j{)}^{\mathrm{\top }}{\mathrm{\Omega }}_k{\mathbf{\text{e}}}_k({\mathbf{\text{x}}}_i,{\mathbf{\text{x}}}_j),\cdots \cdots (4.16)$$

수식을 풀면,

$${\mathbf{\text{x}}}^{\ast }=\underset{\mathbf{\text{x}}}{\mathrm{argmin}}\sum _{k=1}^K{\mathbf{\text{e}}}_k({\mathbf{\text{x}}}_i,{\mathbf{\text{x}}}_j{)}^{\mathrm{\top }}{\mathrm{\Omega }}_k{\mathbf{\text{e}}}_k({\mathbf{\text{x}}}_i,{\mathbf{\text{x}}}_j)\cdots \cdots (4.17)$$

마지막으로 주목해야 할 점은 ${\mathbf{\text{F}}}_k=-log{\varphi }_k$ 용어가 오차 ${\mathbf{\text{e}}}_k={\mathbf{\text{e}}}_k({\mathbf{\text{x}}}_{i_k},{\mathbf{\text{x}}}_{j_k})$의 제곱 마할라노비스 거리보다 작지 않다는 것이다.

이는 다음과 같은 형식과 표기를 가진다.

$${\mathbf{\text{F}}}_k\propto -log{\varphi }_k\propto {\mathbf{\text{e}}}_k^{\mathrm{\top }}{\mathrm{\Omega }}_k{\mathbf{\text{e}}}_k={\Vert {\mathbf{\text{e}}}_k\Vert }_{{\mathrm{\Omega }}_k^{-1}}^2={\Vert {\mathrm{\Omega }}_k^{\mathrm{\top }/2}{\mathbf{\text{e}}}_k\Vert }^2\cdots \cdots (4.18)$$

A note on motion errors

이 부분에서 핵심은 error를 measurement space에서 정의하는 것이다. 

생각해 보면 우리는 지금까지 motion model을 
$$\mathbf{e}=\mathbf{f}({\mathbf{x}}_{i-1},{\mathbf{u}}_i)-{\mathbf{x}}_i$$
와 같이 정의했다.
사실 위와 같이 정의한 것은 state space에서의 정의이며 다음과 같은 motion model을 고려하여 나타난다.
$${\mathbf{x}}_i=f_x({\mathbf{x}}_{i-1},{\mathbf{u}}_i)+{\mathbf{w}}_i^{\prime },{\mathbf{w}}_i^{\prime }\sim \mathcal{N}\{0,{\mathrm{\Omega }}^{\prime -1}\}$$

하지만 noise $\mathbf{w}$는 measurements $u$와 관련이 있다.

따라서 다음과 같다.

$${\mathbf{x}}_i=f_u({\mathbf{x}}_{i-1},{\mathbf{u}}_i-{\mathbf{w}}_i),{\mathbf{w}}_i\sim \mathcal{N}\{0,{\mathrm{\Omega }}^{-1}\}$$

 

여기에서 ${\mathbf{w}}_i^{{}^{\prime }}$는 state space에서의 noise이다.
로봇의 상태가 제어입력과 상관없이 변경될 수 있는 불확실성을 나타낸다. 
${\mathrm{\Omega }}^{{}^{\prime }}$는 jacobian의 랭크에 따라 singularity 특성을 가질 수 있고 이는 계산이 어렵다.

${\mathbf{w}}_i$는 measurement space에서의 noise이다.
로봇의 상태가 제어입력과 직접 적용된다. 
이는 다른 말로 제어입력이 정확하지 않음을 의미한다.
$\mathrm{\Omega }$는 보통 fullrank이며 계산이 용이하다.

 

그래서 잘 정의된 정보행렬 $\mathrm{\Omega }$를 가진 error $\mathbf{e}$를 정의하기 위해 모션 모델의 역함수를 정의한다.

$${\mathbf{u}}_i=f^{-1}({\mathbf{x}}_i,{\mathbf{x}}_{i-1})+{\mathbf{w}}_i\cdots \cdots (4.19)$$

$f()$가 $x_{i-1}$과 $u_i$를 이용하여 현재 상태 $x_i$를 추정한다면,
$f({)}^{-1}$은 반대로 생각해서(식 4.19와 같이) $x_i$와 $x_{i-1}$을 알고있을때 제어입력 $u_i$를 추정하는 것이다.

따라서 error는 다음과 같이 정의한다.

$$\mathbf{e}=f^{-1}({\mathbf{x}}_i,{\mathbf{x}}_{i-1})-{\mathbf{u}}_i\cdots \cdots (4.20)$$

위 식은 예측된 제어입력과 실제 제어 입력의 차이로 error를 정의하는 식이다.

그리고 measurement space에서 정의된 error로 볼 수 있다.

 

예제로 IMU motion integration과 같은 복잡한 상황을 다루는 것을 제시한다.

여기에서는 modified measurement $\mathbf{z}=z(\mathbf{u})$를 사용해서 function $g$를 다음과 같이 정의한다.

landmark measurements,

$$\mathbf{e}=h({\mathbf{x}}_i,{\mathbf{l}}_j)-\mathbf{z}$$

$${\mathbf{z}}_i=g({\mathbf{x}}_i,{\mathbf{x}}_{i-1})+{\mathbf{w}}_i\cdots \cdots (4.21)$$

$$\mathbf{e}=g({\mathbf{x}}_i,{\mathbf{x}}_{i-1})-{\mathbf{z}}_i\sim \mathcal{N}(0,{\mathrm{\Omega }}^{-1})\cdots \cdots (4.22)$$

이렇게 함으로써 복잡한 모션 데이터를 다룰 수 있다.

4.2 Iterative non-linear optimization

잠깐 최적화에 대해 이야기하는 섹션이다.

사실 기본적인 최적화 방법인 가우시안 뉴턴에서 LM방법까지 잘 알고 있다면 생략해도 되는 섹션이다.

자 이제 간단한 기초 내용을 살펴보고 여러 방법을 알아보자.

 

어떤 cost function $\mathbf{F}(\mathbf{x})$가 있다고 해보자.

최적의 state ${\mathbf{x}}^{\ast }$는 cost를 최소화하는 것일 테니 다음과 같이 정의된다.

$${\mathbf{x}}^{\ast }=\arg \underset{\mathbf{x}}{min}F(\mathbf{x})\cdots \cdots (4.23)$$

모든 iterateve optimization 방법은 step을 가지고 반복적으로 해에 접근한다.

그 과정에서 $\mathrm{\Delta }\mathbf{x}$를 이용해서 ${\mathbf{x}}_n={\mathbf{x}}_{n-1}+\mathrm{\Delta }{\mathbf{x}}_n$이 최적의 ${\mathbf{x}}^{\ast }$에 수렴한다.

4.2.1 The general case and the Newton method

Fig. 4.4에 나온 것처럼 step마다 $\mathrm{\Delta }\mathbf{x}$가 존재한다.

fig. 4.4

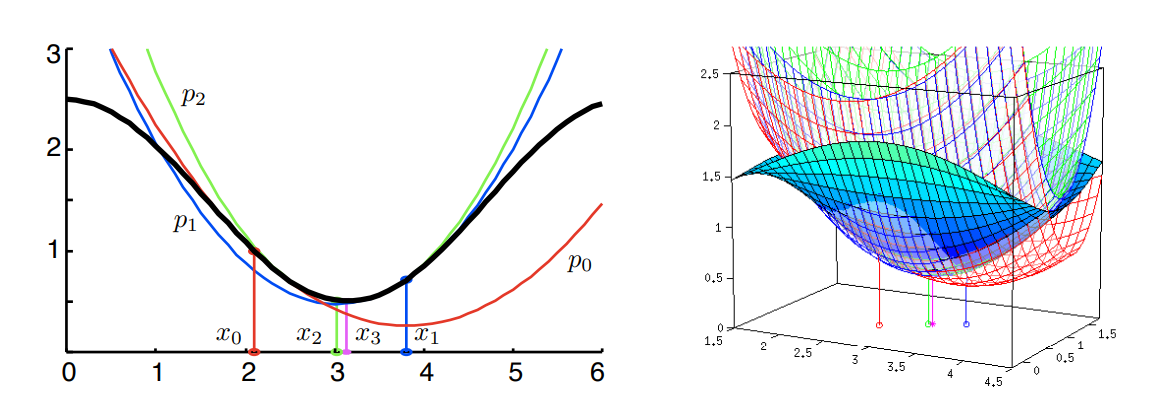
Fig. 4.4는 iterative Newron step을 이용해서 nonlinear optimization문제를 해결하는 과정을 보인다.

검은색의 비선형 함수가 있을 때, 이 함수의 minimum$x^{\ast }$은 $\pi$이다.
$x_0$의 초기값에서 2차 함수로 근사를 하고 그 최솟값 $x_1$에서 또 다시 검은색의 비선형 함수에 대해 2차함수 근사를 한다.
이렇게 2차 함수로 근사하고 그 최솟값에서 다시 2차함수로 근사하며 점점 해에 다가간다.

오른쪽 figure도 이와 동일한 방법으로 매쉬 형태를 가진 함수로 하는 과정이다.

 

2차 테일러 전개를 통해 현재 추정치에서 cost의 local parabolic 근사를 다음과 같이 나타낸다.

$$F(\breve{\mathbf{x}}+\mathrm{\Delta }\mathbf{x})\approx F(\breve{\mathbf{x}})+\mathrm{\nabla }F\mathrm{\Delta }\mathbf{x}+\frac{1}{2}\mathrm{\Delta }{\mathbf{x}}^{\mathrm{\top }}{\mathbf{H}}_F\mathrm{\Delta }\mathbf{x}\cdots \cdots (4.24)$$

$\mathrm{\nabla }F$와 ${\mathbf{H}}_F$는 각각 $F$의 gradient vector와 Hessian matrix이다.

$$\mathrm{\nabla }F\triangleq {\frac{\partial F}{\partial \mathbf{x}}|}_{\breve{\mathbf{x}}}\cdots \cdots (4.25)$$

$${\mathbf{H}}_F\triangleq {\frac{{\partial }^{2}F}{\partial {\mathbf{x}}^2}|}_{\breve{\mathbf{x}}}\cdots \cdots (4.26)$$

그리고 최적 스텝 $\mathrm{\Delta }{\mathbf{x}}^{\ast }$은 식 (4.24)를 미분하고 0과 같다고 놓으면 다음과 같이 주어진다.

 $$\mathrm{\nabla }{F}^{\mathrm{\top }}+{\mathbf{H}}_F\mathrm{\Delta }{\mathbf{x}}^{\ast }=0\cdots \cdots (4.27)$$

그리고 Newton step을 도출한다.

$$\mathrm{\Delta }{\mathbf{x}}_N^{\ast }=-({\mathbf{H}}_F{)}^{-1}\mathrm{\nabla }{F}^{\mathrm{\top }}\cdots \cdots (4.28)$$

 

Newton method는 초기 추정치가 해와 가까우면 빠르게 수렴한다.
초기추정치가 해와 멀면 수렴이 불안정해진다.

또한 두 가지 중요한 단점이 존재한다.

hessian matrix에 대한 개념이 필요하다.

헤세 행렬(Hessian Matrix)의 기하학적 의미 - 공돌이의 수학정리노트 (Angelo's Math Notes)

 

1. step의 길이가 긴 경우 local minimum에 빠질 수 있다.
   이 경우는 ${\mathbf{H}}_F$가 너무 작은 경우 발생한다.
   너무 작은 경우는 cost $F(\mathbf{x})$가 낮은 곡률을 가질 때다.
   이럴때 step이 크게 계산되며 최적화가 실패하고 잘못된 지점으로 이동할 수 있다.
2. 오목한 영역에서의 문제
   오목한 영역에서는 ${\mathbf{H}}_F$일부 혹은 전체가 음수가 된다.
   ${\mathbf{H}}_F$가 음수인 경우 step이 반대 방향으로 진행될 수 있다.
   즉, 비용을 증가시키는 방향으로 이동하며, 최솟값에서 멀어진다.
   이렇게 되면 최적화가 실패한다.

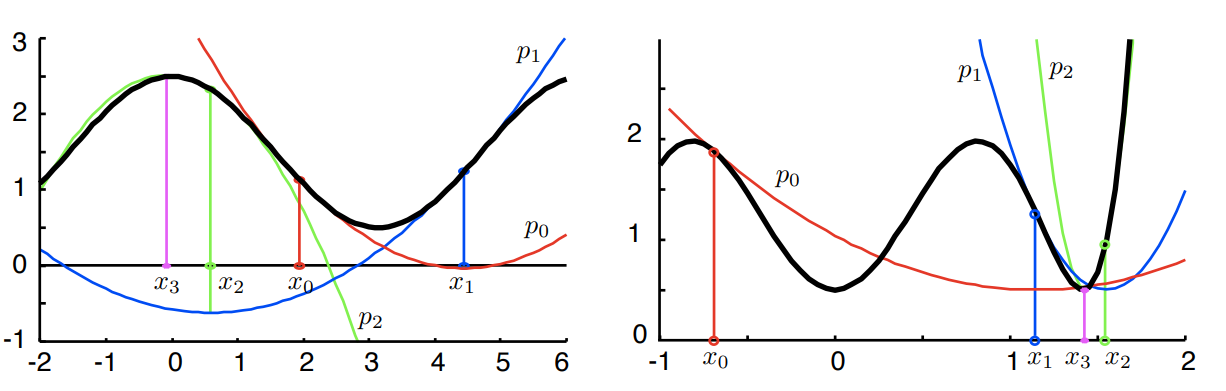
이러한 두 가지 단점은 fig. 4.5 왼쪽 그림에 나와있다(실패 상황).

오른쪽 그림은 안정적으로 수렴하는 과정을 보인다.

fig. 4.5

4.2.2 The least squares case and the Gauss-Newton method

많은 상황에서 cost function은 error $\mathbf{e}(\mathbf{x})$의 제곱 함수로 표현된다.

$$F(\mathbf{x})=\frac{1}{2}\mathbf{e}(\mathbf{x}{)}^{\mathrm{\top }}\mathbf{\Omega }\mathbf{e}(\mathbf{x})\cdots \cdots (4.29)$$

$\mathrm{\Omega }$는 symmetric하고 positive-definite matrix이다.

그렇다면 gradient vector $\mathrm{\nabla }F$와 Hessian matrix ${\mathbf{H}}_F$는 다음과 같이 주어진다.

$$\mathrm{\nabla }F={\frac{\partial F}{\partial \mathbf{x}}|}_{\breve{\mathbf{x}}}=\left({\mathbf{e}}^{\mathrm{\top }}\mathbf{\Omega }\frac{\partial \mathbf{e}}{\partial \mathbf{x}}\right){|}_{\breve{\mathbf{x}}}={\breve{\mathbf{e}}}^{\mathrm{\top }}\mathbf{\Omega }\mathbf{J}\cdots \cdots (4.30)$$

$${\mathbf{H}}_F={\frac{{\partial }^{2}F}{\partial {\mathbf{x}}^2}|}_{\breve{\mathbf{x}}}=(\frac{\partial {\mathbf{e}}^{\mathrm{\top }}}{\partial \mathbf{x}}\mathbf{\Omega }\frac{\partial \mathbf{e}}{\partial \mathbf{x}}+{\mathbf{e}}^{\mathrm{\top }}\mathbf{\Omega }\frac{{\partial }^2\mathbf{e}}{\partial {\mathbf{x}}^2}){|}_{\breve{\mathbf{x}}}={\mathbf{J}}^{\mathrm{\top }}\mathbf{\Omega }\mathbf{J}+{\breve{\mathbf{e}}}^{\mathrm{\top }}\mathbf{\Omega }\mathcal{H}\cdots \cdots (4.31)$$

$\breve{\mathbf{e}}$, $\mathbf{J}$와 $\mathcal{H}$는 모두 current state estimate $\partial \mathbf{x}$의 error와 일차 이차 도함수를 나타낸다.

$$\breve{\mathbf{e}}\triangleq \mathbf{e}(\breve{\mathbf{x}})\cdots \cdots (4.32)$$

$$\mathbf{J}\triangleq {\frac{\partial \mathbf{e}}{\partial \mathbf{x}}|}_{\breve{\mathbf{x}}}\cdots \cdots (4.33)$$

$$\mathcal{H}\triangleq {\frac{{\partial }^2\mathbf{e}}{\partial {\mathbf{x}}^2}|}_{\breve{\mathbf{x}}}\cdots \cdots (4.34)$$

• 식 (4.32) : 열 벡터
• 식 (4.33) : 1차 도함수의 jacobian matrix
• 식 (4.34) : 2차 도함수의 hessian tensor

Cost에 대한 지역적 이차 근사에 따르면 form은 다음과 같다.

$$F(\breve{\mathbf{x}}+\mathrm{\Delta }\mathbf{x})\approx \frac{1}{2}{\breve{\mathbf{e}}}^{\mathrm{\top }}\mathbf{\Omega }\breve{\mathbf{e}}+{\breve{\mathbf{e}}}^{\mathrm{\top }}\mathbf{\Omega }\mathbf{J}\mathrm{\Delta }\mathbf{x}+\frac{1}{2}\mathrm{\Delta }{\mathbf{x}}^{\mathrm{\top }}({\mathbf{J}}^{\mathrm{\top }}\mathbf{\Omega }\mathbf{J}+{\breve{\mathbf{e}}}^{\mathrm{\top }}\mathbf{\Omega }\mathcal{H})\mathrm{\Delta }\mathbf{x}\cdots \cdots (4.35)$$

hessian ${\mathbf{H}}_F$의 항이 식 (4.31)에서 ${\mathbf{J}}^{\mathrm{\top }}\mathbf{\Omega }\mathbf{J}+{\breve{\mathbf{e}}}^{\mathrm{\top }}\mathbf{\Omega }\mathcal{H}$였다.

여기에서 두 번째 항 ${\breve{\mathbf{e}}}^{\mathrm{\top }}\mathbf{\Omega }\mathcal{H}$은 무시가 가능하다.

왜냐하면 $\breve{\mathbf{e}}$와 $\mathcal{H}$가 무시할 정도로 작기 때문이다.

계산이 복잡하고 다루기 어려울 수 있는데 덕분에 한결 나아진다.

간소화를 적용하면 Gauss-Newton 의 cost function은 다음과 같다.

$$F(\breve{\mathbf{x}}+\mathrm{\Delta }\mathbf{x})\approx \frac{1}{2}{\breve{\mathbf{e}}}^{\mathrm{\top }}\mathbf{\Omega }\breve{\mathbf{e}}+{\breve{\mathbf{e}}}^{\mathrm{\top }}\mathbf{\Omega }\mathbf{J}\mathrm{\Delta }\mathbf{x}+\frac{1}{2}\mathrm{\Delta }{\mathbf{x}}^{\mathrm{\top }}{\mathbf{J}}^{\mathrm{\top }}\mathbf{\Omega }\mathbf{J}\mathrm{\Delta }\mathbf{x}\cdots \cdots (4.36)$$

Error에 대해 선형 근사를 하면 $\mathbf{e}(\breve{\mathbf{x}}+\mathrm{\Delta }\mathbf{x})\approx \breve{\mathbf{e}}+\mathbf{J}\mathrm{\Delta }\mathbf{x}$이고 식 (4.29)에 대체하면, hessian $\mathbf{H}$는 다음과 같다.

$$\mathbf{H}\triangleq {\mathbf{J}}^{\mathrm{\top }}\mathbf{\Omega }\mathbf{J}\approx {\mathbf{H}}_F\cdots \cdots (4.37)$$

Gauss-Newton step은

$$\mathrm{\Delta }{\mathbf{x}}_{\text{GN}}^{\ast }=-{\mathbf{H}}^{-1}\mathrm{\nabla }{F}^{\mathrm{\top }}\cdots \cdots (4.38)$$

또는 gradient vector $\mathrm{\nabla }F$와 Hessian matrix ${\mathbf{H}}_F$를 각자의 식으로 표현하면 다음과 같다.

$$\mathrm{\Delta }{\mathbf{x}}_{\text{GN}}^{\ast }=({\mathbf{J}}^{\mathrm{\top }}\mathbf{\Omega }\mathbf{J}{)}^{-1}{\mathbf{J}}^{\mathrm{\top }}\mathbf{\Omega }\breve{\mathbf{e}}\cdots \cdots (4.39)$$

Jacobian $\mathbf{J}$의 left weighted generalized inverse로 알려진 ${\mathbf{J}}_{\mathbf{\Omega }}^{+}$
$${\mathbf{J}}_{\mathbf{\Omega }}^{+}\triangleq ({\mathbf{J}}^{\mathrm{\top }}\mathbf{\Omega }\mathbf{J}{)}^{-1}{\mathbf{J}}^{\mathrm{\top }}\mathbf{\Omega }\cdots \cdots (4.40)$$을 적용하면 다음과 같다.

$$\mathrm{\Delta }{\mathbf{x}}_{\text{GN}}^{\ast }=-{\mathbf{J}}_{\mathbf{\Omega }}^{+}\breve{\mathbf{e}}\cdots \cdots (4.41)$$

이것으로 step이 observed error $\breve{\mathbf{e}}$에 비례함을 알 수 있다.

• $J$이 full column rank일 때 ${\mathbf{J}}_{\mathbf{\Omega }}^{+}$를 계산 가능하다. 그렇지 않은 경우에는 generalized inverse를 이용해야 한다. Generalized inverse 는 주어진 행렬이 역행렬을 가지지 않더라도 가능한 최선의 근사치로 정의된다.
  ${\mathbf{J}}_{\mathbf{\Omega }}^{\mathrm{\#}}\triangleq ({\mathbf{J}}^{\mathrm{\top }}\mathbf{\Omega }\mathbf{J}{)}^{+}{\mathbf{J}}^{\mathrm{\top }}\mathbf{\Omega }$

Weighted inverse ${\mathbf{J}}_{\mathbf{\Omega }}^{+}$은 계산 비용이 많이 들기 때문에 복잡도를 줄이기 위해 다음과 같은 방법을 사용한다.

• Weighted jacobian ${\mathbf{\Omega }}^{-\mathrm{\top }/2}\mathbf{J}$에 대해 QR factorization(QR decomposition)을 한다.
• Approximate Hessian $\mathbf{H}$에 대해 Cholesky factorization을 한다.

$\mathbf{H}={\mathbf{J}}^{\mathrm{\top }}\mathbf{\Omega }\mathbf{J}$은 Hessian matrix ${\mathbf{H}}_F$의 근사이다. 종종 이걸 Hessian matrix라고 부르는 경우가 많은데, 정확한 표현으로는 ${\mathbf{\Omega }}^{-\mathrm{\top }/2}\mathbf{J}$ 열들의 Grammian matrix이다. (저자가 grammian matrix라고 언급. gram matrix가 보편적인 듯 하다.)

grammian matrix는 행렬의 열 벡터들의 내적을 통해 만들어진다.

Gaussian 분포의 경우, 행렬 $\mathbf{H}$는 information matrix로 해석할 수 있다.

Information matrix는 변수 $\mathrm{\Delta }x$의 공분산의 역행렬과 일치한다.

$\mathbf{H}$의 역할로 'Hessian', 'Grammian(Gram)', 'Information' matrix을 소개했는데 이는 앞으로 나올 Cholesky factorization 방법에서 중요한 역할을 한다. 

Gauss-Newton 방법은 Newton 방법과 똑같은 단점을 가지지만 다른점이 있다.

Gauss-Newton 방법에서는 수정된 헤시안 행렬 $\mathbf{H}$이 항상 양수이기 때문에 최대값으로 수렴하지 않는다는 점이 다르다.

Hessian matrix가 항상 양수이니까 곡률에 대한 정보는 최솟값밖에 없다는 뜻이다.

나머지 단점은 위에서 언급한 Newton 방법에서와 동일하다 : )

4.2.3 Improving convergence with the Levenberg-Marquardt(LM) algorithm

앞서 살펴본 Newton-based 방법들은 다음과 같은 단점을 가지고 있었다.

• 초기값이 최적에 가까운 경우에 효과적이다.
• 최적점에서 멀어지면 근사한 포물면이 최소값의 형태에 맞지 않고 계산된 step이 부적절할 수 있다.
• Hessian matrix의 곡률이 작으면, step이 매우 커지며 최적화가 불안정해질 수 있고 최적값에서 멀어질 수 있다.

LM 알고리즘은 Levenberg의 idea를 Marquardt가 보완한 것이다.

최적 해로부터 멀리 떨어져 있을 때 gradient decent 방법으로 접근하고 최적 해 근처에서는 Gauss-Newton 방식으로 동작한다.

Gauss-Newton보다 안정적인 수렴을 보여주기 때문에 비선형 최적화 문제에서는 일반적으로 많이 사용된다고 한다.

한 번 살펴보자.

 

Levenberg

Levenberg의 key idea는 Hessian에 damping(감쇠)를 줘서 Gauss-Newton step을 수정했다는 것이다.

$$\mathrm{\Delta }{\mathbf{x}}_L^{\ast }=-\alpha (\mathbf{H}+\lambda \mathbf{I}{)}^{-1}\mathrm{\nabla }{F}^{\mathrm{\top }}\cdots \cdots (4.42)$$

여기에서 $\lambda$가 작을경우 Gauss-Newton step에 따라 진행되고, $\lambda$가 클경우 step은 gradient $\mathrm{\nabla }{F}^{\mathrm{\top }}={\mathbf{J}}^{\mathrm{\top }}\mathbf{\Omega }\breve{\mathbf{e}}$의 영향을 크게 받으면서 gradient descent 알고리즘이 된다.

파라미터 $\alpha$는 step의 길이와 관련이 있다.

Marquardt

Marquardt는 Levenberg 아이디어의 damping matrix를 identity matrix $I$에서 Hessian matrix $H$의 대각 행렬로 변경했다.

이렇게 함으로써 비용 함수의 곡률에 따라 상태의 각 방향에 다른 감쇠를 적용한다.

$$\mathrm{\Delta }{\mathbf{x}}_{LM}^{\ast }=-\alpha (\mathbf{H}+\lambda \mathrm{diag}(\mathbf{H}){)}^{-1}\mathrm{\nabla }{F}^{\mathrm{\top }}\cdots \cdots (4.43)$$

$\lambda$와 $\alpha$는 지속적으로 조정되며, $\lambda$는 감쇠항을 조절하고 $\alpha$는 스텝 크기를 조절한다.

4.2.4 The sparse structure of the SLAM problem

작성중...

추가 내용 작성 중

24.6~

본 내용은 Joan Sola님의 Course on SLAM의 내용을 주로 참고하여 작성했습니다.

[reference]

1. 다크프로그래머

함수최적화 기법 정리 (Levenberg–Marquardt 방법 등)

 

오류가 있다면 댓글을 남겨주세요~