GVINS 논문 요약

 

GVINS?

최근 실외 자율주행을 연구하기로 결심하면서 장시간 실외 주행에서도 강인함을 보여주는 SLAM알고리즘을 탐색했다. 

실외 자율주행에서 Visual-Inertial SLAM은 어려운 도전과제이다.

특히 대표적인 단점으로는 long-term 주행 시 누적되는 drift가 상당하다는 점이다.

이를 해결하기 위해서 GNSS 메세지를 수신받아 fusion 하여 trajectory의 정밀도를 올려준다.

 

논문의 정확한 이름은 Tightly Coupled GNSS-Visual-Inertial Fusion for Smooth and Consistent State Estimation이다.

GVINS: Tightly Coupled GNSS–Visual–Inertial Fusion for Smooth and Consistent State Estimation

GitHub - HKUST-Aerial-Robotics/GVINS: Tightly coupled GNSS-Visual-Inertial system for locally smooth and globally consistent sta

GVINS의 front-end를 구성하는 VINS-mono의 요약 리뷰는 아래 블로그를 추천한다! 

[Paper Review] VINS-mono 요약 및 설명

만약 VINS-mono를 디테일하게 살펴보고 싶다면 아래 블로그를 추천한다!

특히 어려운 개념인 IMU preintegration에 대해서 시각화 및 설명이 잘 되어있다.

[SLAM] VINS-mono 논문 리뷰 (+ IMU preintegration)

혹시라도 수식이 이상하게 보인다면

1. 아무 수식에 오른쪽 마우스 클릭

2. Math settings -> Math Renderer -> SVG

3. 새로고침

1. Introduction

대표적으로 lidar를 쓰거나 camera를 쓰는 SLAM방식으로 나뉜다.

둘 중에 camera는 저비용 장치라서 CV와 robotics분야에서 꽤 많은 관심을 받고 있다.

Camera에 IMU를 결합하는 방식은 복잡한 환경에서도 보다 강인하고 정밀도가 있는 수준을 제공한다.

 

하지만, camera와 IMU는 local frame에서 작동하며 VIN(Visual-Inertial Navigation)에서 x, y, z, yaw 네 가지 방향이 관측하기 어려움이 증명되었다.

그래서 odometry drift는 VIN시스템에서 불가피한 현상이다.

반면에 GNSS는 localization에서 drift-free 하며 global-aware 한 해결책을 제시해 준다.

GNSS 수신기와 위성 사이의 전파 신호를 이용하며 거리 정보를 주고받는다.

최소 4개의 위성이 tracked 된다면 수신기는 global Earth frame에서 고유한 위치값을 얻을 수 있게 된다.

이렇게 GNSS와 VIN이 결합되었을 때 좋은 시너지를 낼 것으로 보였다.

 

하지만, 센서를 fusion 하는 과정에서 많은 어려운 상황이 발생한다.

 

첫 번째, noisy 한 특성의 GNSS로부터 안정적인 초기화가 반드시 필요하다.

특히 VIN데이터가 얻어지는 local frame과 GNSS 데이터가 얻어지는 global frame사이의 4-DOF 변환이 중요하다.

이 변환은 camera와 IMU의 extrinsic 변환과는 다르게 offline calibrated 될 수 없다.

왜냐하면 VIN 시스템이 시작될 때마다 변환이 변하기 때문이다.

게다가, one-shot alignment는 GNSS 중단 상황에서는 융합 시스템의 drift로 인해 정렬이 무효화된다.

그래서 local frame과 global frame의 onlie 초기화 과정이 필요하다.

 

두 번째, GNSS 측정값은 VIN 시스템과 동일한 정밀도 순서가 아니며, GNSS 신호 전파 과정에서 다양한 에러 원인이 존재한다.

실제로, global localization에 사용되는 code pseudorange 측정값은 오직 meter-level의 정밀도를 가지고 있다.

반면에 VIN시스템은 짧은 범위에서 centimeter-level의 예측 결과를 제공한다.

따라서 적절히 처리되지 않는다면 퓨전은 노이즈가 있는 GNSS 측정값의 영향을 받을 수 있다.

 

세 번째, 시스템이 pure rotation(제자리 회전)을 겪거나 추적 중인 위성의 수가 충분하지 못한 경우(4개 미만) GNSS degenerate가 발생하게 된다. 예를 들면 실내에서 실외환경으로 장소가 바뀔 때, 추적에 실패한 위성 신호를 다시 얻게 되는 과정이 있다.

 

앞서 말한 이슈를 해결하기 위해, 저자는 GNSS raw 측정값과 visual, inertial 데이터를 tightly fuse 해서 정확도와 드리프트가 보완된 state estimation을 가능하게 하는 non-linear optimization-based 시스템을 제안한다.

Local frame과 global frame 사이의 4-DOF변환은 초기화 단계에서 coarse-to-fine 접근을 통해 복원되며, 이후에 추가적으로 최적화된다.

노이즈가 존재하는 GNSS raw 측정값을 위해, 모든 GNSS 제약들이 확률적 factor graph 아래 표현되며 이는 jointly optimized 된다.

게다가, GNSS degenerate 상황은 시스템의 강인함을 위해 조심스럽게 다뤄지며 논의된다.

tightly coupled 방식과 시스템 설계 덕분에, 시스템은 GNSS와 visual, inertial 특성을 완전히 활용한다.

그리고 복잡한 환경에서도 지역적으로 부드럽고 전역적으로 일관된 추정을 제공한다.

이를 Fig. 1에서 확인할 수 있다.

Fig. 1. Snapshot of our system in a complex indoor–outdoor environment. The global estimation result is plotted on Google Maps directly and aligns well with the ground truth RTK trajectory, as shown in (a). (b) Depicts the distribution of satellites, with the tangential direction representing the azimuth and radial direction being the elevation angle. The blue arrow is a compass-like application, which indicates the global yaw orientation of the camera. Subplots (c) and (d) illustrate the altitude information and the local-ENU yaw offset, respectively. The measurement noise level of each tracked satellite is shown in (e). Note that there is an obvious failure on the RTK trajectory when we walk on indoor stairs, while our system can still perform global estimation even in the indoor environment.

논문에서 contribution은 다음과 같다.

1) GNSS와 visual, inertial state를 초기화하기 위한 online coarse-to-fine 접근

2) 확률적 프레임워크 하에 다중 위성신호를 받아들이는 GNSS raw 측정값과 visual-inertial fuse를 optimization-based tightly-coupled 접근

3) GNSS 신호가 차단되거나 접근 불가능한 복잡한 환경에서 drift 없는 6-DOF global 추정이 가능한 실시간 추정기

4) 제안한 시스템을 시뮬레이션과 실제 환경에서 광범위하게 평가

4. GNSS Fundamentals

GVINS에서는 새로운 개념인 GNSS 데이터가 등장한다.

우리가 흔히 알고 있는 GPS는 GNSS의 한 종류이며 그렇게 부르는 게 맞으나, 보통 GPS라고 부르기도 한다.

 

논문에서는 GNSS에 생소한 독자를 위해 GNSS fundamentals라는 섹션을 따루 두었다.

처음 이해하기 힘들 수 있으나 인터넷에 떠도는 정보들을 더 보고 나면 어느 정도 이해가 될 것이다.

 

정확한 이해가 중요하기 때문에 요약보다는 번역을 해두었다.

A. GNSS Overview

GNSS는 이름이 알려주듯이 위성 기반의 시스템이다.

위성은 우리가 지구 어디쯤에 있는지 경도, 위도, 고도라는 global localization 서비스를 제공한다.

이 위성 쏘아 올리고 서비스를 제공하는 대표적인 나라가 있는데 아래와 같다.

• GPS : 미국
• GLONASS : 러시아
• Galileo : 유럽연합
• BeiDou : 중국

물론 한국, 일본, 인도 같은 나라도 있다.

 

이 위성들은 지금도 지구 20,000km 상공에서 궤도를 돌며 여러 정보가 담긴 전파를 지속적으로 방송한다.

 

GVINS 시스템에서는 GPS L1 signal을 사용하기 때문에 예시를 L1C signal로 설명해 뒀다.

Fig. 3에 나와있듯이 L1C signal은 세 개의 레이어로 구성되어 있다.

Fig. 3. Hierarchical structure of the GPS L1C signal. The navigation message first mixes with the satellite-specific PRN code, and then, the resulting sequence is used to modulate the high-frequency carrier signal. The final signal is transmitted by the satellite and captured by the receiver, which applies a reverse process to obtain the measurement and retrieve the message.

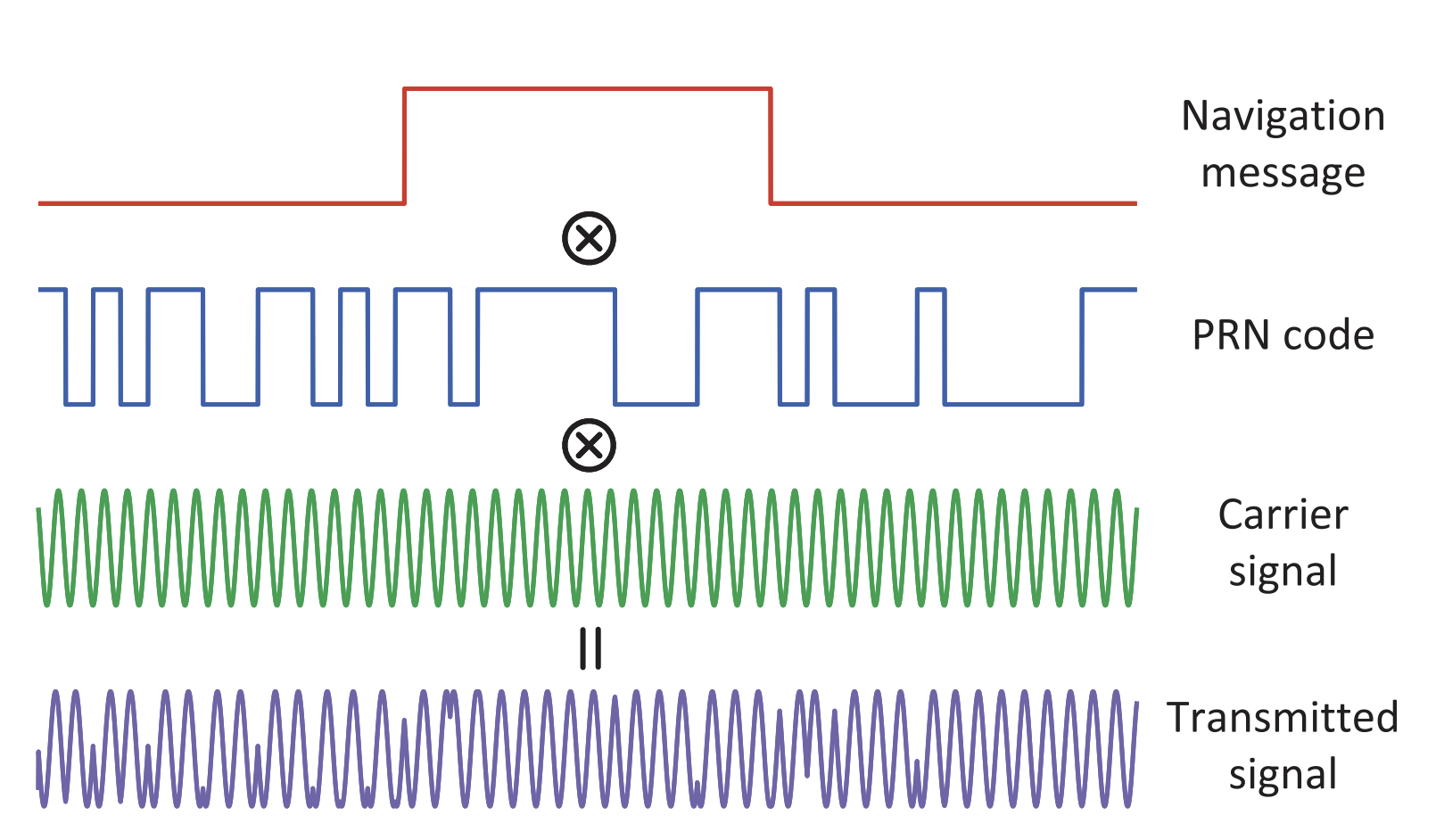
항법 메시지(L1C signal)는 궤도, 시계 오차 보정계수, 이온권 지연 계수 및 위성 상태와 관련된 기타 정보가 포함되어 있다.

Ephemeris라고 알려진 궤도 파라미터는 14개의 변수를 포함하고 있으며 특정 시간에서 위성의 ECEF좌표를 계산하기 위해 사용된다.

위성의 시계 오차는 세 개의 파라미터를 가진 2차 다항식으로 모델링 된다.

각 위성은 1 ms 마다 반복되는 고유한 PRN(pseudorandom noise) code를 부여받는다.

50-bit/s의 항법 메시지는 먼저 PRN code와 exclusive-OR 연산을 하고 고주파를 띄는 반송파를 변조한다.

Signal을 수신하고 난 후, 수신한 Signal과 설계된 signal의 주파수 차이를 통해 Doppler shift를 얻는다.

Code pseudorange measurement는 PRN code의 shift로 유추되며, 이는 전파된 시간을 의미한다.

마지막으로, 항법 메시지의 변조된 반송파를 재구성하여 값을 얻는 과정을 거친다.

B. Code Pseudorange Measurement

A파트에서 말했듯이 PRN code의 shif를 통해 ToF(Time of Flight)를 측정할 수 있다.

ToF를 알고 거기에 빛의 속도를 곱한다면?

거리 = 속도 x 시간이니까 거리값을 알 수 있는데 이 것을 code pseudorange measurement라고 한다.

왜 이름에 'pseudo'라는 접두사가 들어가는가?

이 measurement는 위성과 수신기 사이의 거리를 알 수 있을 뿐만 아니라 전파가 생성, 전달, 처리될 때 발생하는 다양한 에러를 담고 있기 때문이다.

위성의 오차 원천은 주로 위성 궤도와 시계 오차로 이루어져 있다.

궤도 오차는 주로 다른 천체의 영향으로 발생하며, ephemeris에 정확히 모델링 되지 않는다.

시계 오차는 위성에 탑재된 원자시계가 표준 시간대에 대해서 완벽하지 않기 때문에 발생한다.

이러한 궤도 오차와 시계 오차는 시스템 제어로 지속적으로 감시되며 수정된다.

 

위성 신호가 전파되는 과정에서 이온층과 대기권을 지나게 된다.

우리가 알고 있는 빛의 속도는 진공상태에서 30만 km이다.

하지만 이온층과 대기권에 있는 이온과 대기상태에 의해서 속도가 감소하게 되는데 이때 신호 지연이 나타난다.

 

신호가 수신기에 다양한 경로로 도달하는 현상을 Multipath 효과라고 한다.

이 효과는 주로 수신기 주변에 반사가 가능한 장애물이 있을 경우 이리저리 반사되며 나타난다.

특히 낮은 고도에 있는 위성의 경우 추가적인 지연이 발생할 수 있다.

 

신호가 도착하면 ToF는 Ts(위성 원자 시계에 의해 표시된 신호 전송시간)과 Tr(수신기의 지역 시간)을 비교하여 계산한다.

Tr은 아까 말했듯이 위성시계와 오차가 존재한다.

따라서, 범위 정보는 수신기의 시계 오차로 인해 GNSS 시스템 시간과의 차이가 발생하게 된다. 

그래서 code pseudorange measurement는 다음과 같이 모델링 될 수 있다.

 

${\mathbf{p}}_s^E$와 ${\mathbf{p}}_r^E$은 각각 위성 $s$와 수신기 $r$의 ECI 좌표이다.

${\zeta }_s$는 4 x 1의 indicator 벡터로써 디자인되었으며, 수신 중인 GNSS는 1로 나머지 세 개는 0으로 설정된다.

$\mathrm{\Delta }{t}^s$는 위성의 시계 오차를 나타내며, 수신하는 항법 메시지로부터 계산할 수 있다.

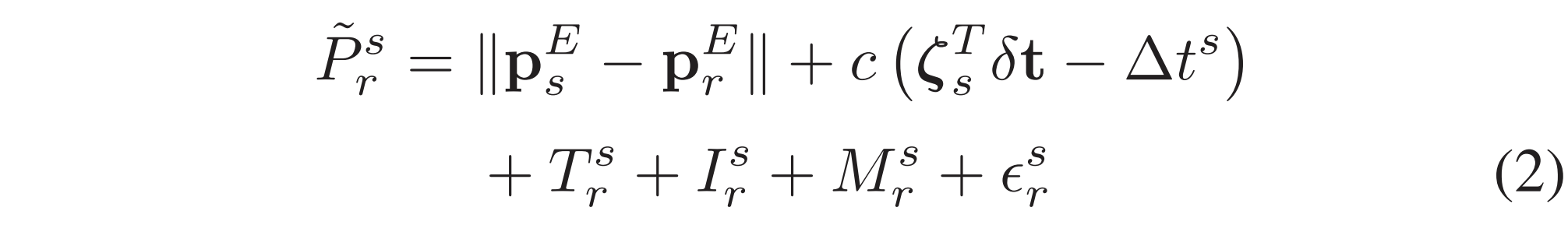
그리고 $T_r^s$와 $I_r^s$는 대류권(tropospheric)과 이온층(ionospheric) delay이다.

$M_r^s$은 multipath 효과에 의한 딜레이로 정의한다.

${ϵ}_r^s$는 measurement noise로 정의한다.

$M_r^s$, $T_r^s$와 $I_r^s$는 길이단위로 표시되며 c로 곱해진다.

 

C. Doppler Measurement

Doppler frequency shift는 수신된 반송파와 설계된 신호 간의 차이를 기반으로 측정되며, 이는 수신기와 위성 간의 신호 전파 경로에서의 상대적인 운동을 반영한다.

이것은 전송 경로를 따른 수신기와 위성 간의 상대적인 움직임을 반영한다.

GNSS signal의 구조적 특성 때문에, doppler 측정값은 대게 code pseudorange보다 한 차원 높다.

Doppler shift는 다음과 같이 모델링 된다.

${\mathbf{v}}_r^E$와 ${\mathbf{v}}_s^E$는 ECI frame에서 수신기와 위성의 속도를 나타낸다.

$\lambda$는 반송파의 파장을 나타내고, ${\kappa }_{\mathbf{r}}^{\mathbf{s}}$는 ECI frame에서 수신기에서 위성으로의 단위 벡터를 나타낸다.

$\dot{\mathrm{\Delta }{t}^s}$는 위성 시계 오차의 drift 비율을 나타내고, 항법 메시지로부터 알 수 있다.

${\eta }_r^s$는 doppler measurement의 노이즈를 나타낸다.

 

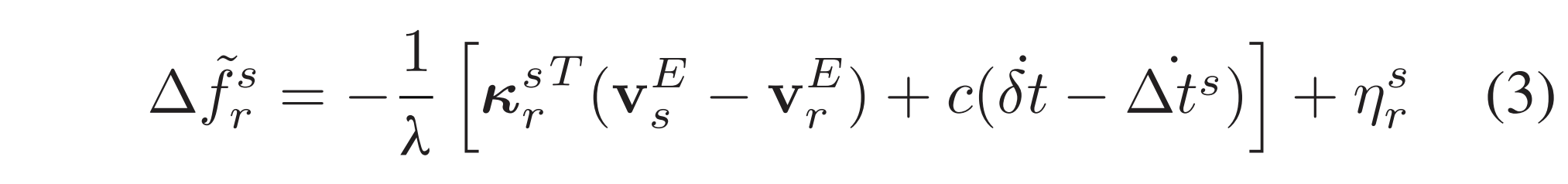
D. SPP Algorithm

SPP 알고리즘은 간단하게 말해서 삼각측량을 통해 GNSS 수신기의 3-DOF global position을 결정하는데, 이때 code pseudorange measurements를 활용한다.

이론적으로 세 개의 위성으로부터 수신기의 위치를 추정할 수 있다.

하지만 B에서 언급한 대로 code pseudorange measurements 측정은 수신기의 시계 bias에 의해 offset 된다.

이러한 시계 bias는 수 백 km의 오차를 유발할 수 있기 때문에 합리적인 결과를 얻기 위해 위치와 함께 추정되어야 한다.

그래서 최소 네 개의 code pseudorange measurements가 필요하며, 3-DOF와 시계 bias를 위해 필요하다.

요약하자면 (N + 3) 개의 위성이 동시적으로 추적되어야 수신기의 위치를 결정지을 수 있다.

N이라고 적힌 것은 저 3개를 제외하고서도 현재 추적되고 있는 위성의 개수이다.

 

충분한 값을 모은 후, 수식 (2)에서 나온 제약조건들을 함께 쌓아서 ${\mathbf{p}}_r^E$와 $\delta \mathbf{t}$가 알려지지 않은 일련의 방정식을 형성한다.

Code pseudorange measurements 보정에 적용되어, 이는 ${\mathbf{p}}_r^E$ 및 $\delta \mathbf{t}$의 함수만으로 나타난다.

GVINS에서는 대류권 delay $T_r^s$를 Saastamoinen 모델을 사용하는 반면, 이온권 delay $I_r^s$는 Klobuchar 모델과 ephemeris 안에 있는 파라미터를 사용하여 계산된다.

특히 GVINS에서는 낮은 고도의 위성을 배제하는 방식으로 multipath 효과를 방지하였다.

이는 식 (2)에서 나온 $M_r^s$를 무시한다는 뜻과 같다.

 

SPP 결과는 측정 노이즈에만 의존하는 게 아니라 위성의 기하학적 배치도 영향을 준다.

저자가 fig. 4에 간단한 2D이미지로 이해 가능하게 올려두었다.

Fig. 4. (a) and (b). Simplified 2-D illustration of how satellite distribution affects the uncertainty of an SPP solution. Here, we assume that the times between the receiver and the satellite are synchronized. Thus, two satellites are enough for localization. The dashed line represents the ground truth range, while the area in between the two solid lines denotes possible noisy measurement. The uncertainties of the SPP solutions are represented by the shadows.

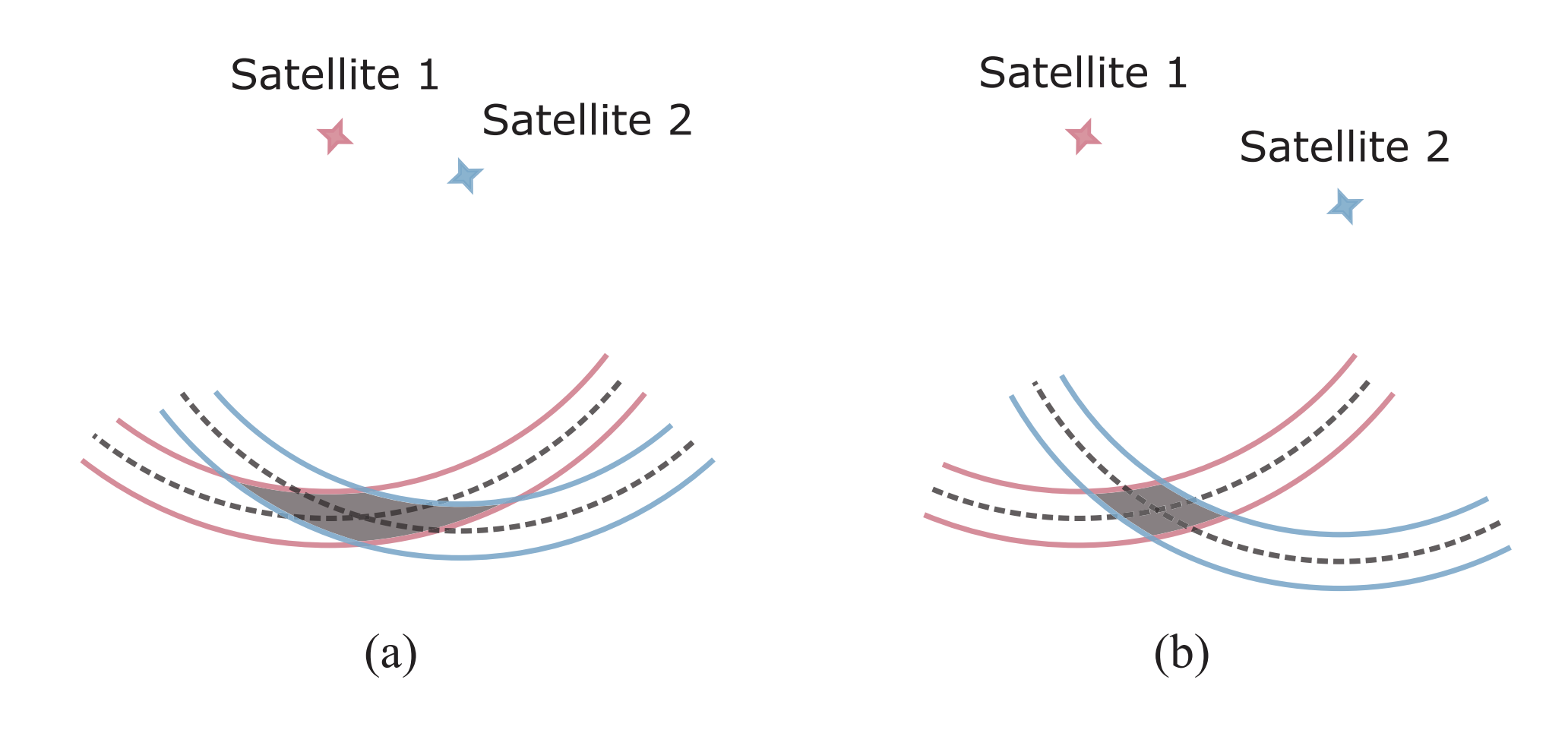
fig. 4에서 설명하는 것처럼 위성이 고르게 분포되어 있으면 측정 노이즈가 변경되지 않더라도 SPP알고리즘의 성능이 향상될 것이다.

5. System Overview

Fig. 5

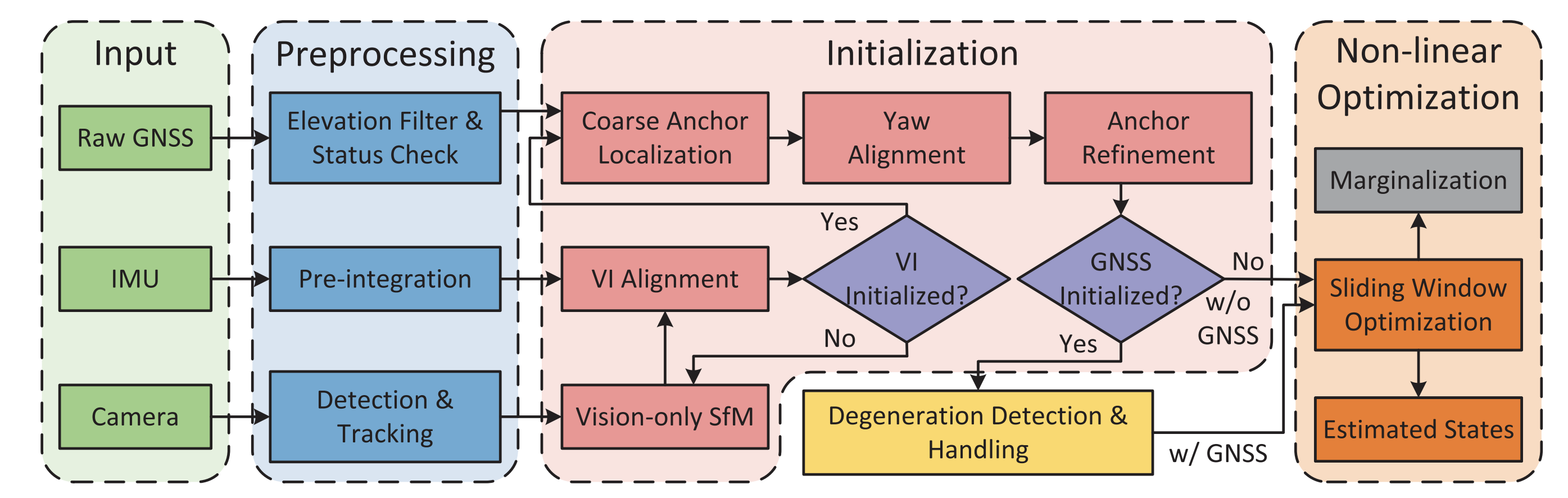
전체 시스템은 위 이미지와 같다.

VINS의 frontend를 기반으로 만들어졌기 때문에 초반에 VI alignment까지는 비슷하다.

GNSS 데이터는 초당 50비트의 속도로 들어오기 때문에 수신하는데 시간이 좀 걸린다.

그래서 GNSS 데이터가 도착할 때까지 해당 데이터는 사용을 하지 못한다.

이후 GNSS데이터를 전처리하고 잘 초기화된 VI와 GNSS를 3단계의 global과 local 정렬을 진행한다.

정렬 과정에서 VI 초기화 과정에서 나온 local 속도와 GNSS doppler 측정을 사용한다고 한다.

그리고 visual, inertial, gnss 등등... 데이터에서 나온 제약들을 sliding window 내에서 비선형 최적화 프레임워크에 구성한다.

실제로 코드의 함수를 보면 ceres solver의 residual block에 제약들을 넣고 state estimation 하는 부분이 있다.

또한 함수에는 최적화하는 부분뿐 아니라 marginalization 부분도 구현되어 있다.

 

만약 GNSS가 이용 불가능할 경우에는 VIO로 전환된다고 한다.

실시간을 보장하고 VI degenerate motions를 다루기 위해 양방향 marginalization 전략을 사용하는데, parallax test에 기반하여 프레임을 제거한다.

6. Probablistic Formulation

GVINS에서 전체 문제는 factor graph로 구성되며, 센서의 측정값은 일련의 factor를 형성하여 시스템의 state를 제약한다.

그래서 probabilistic graph안의 factor에 대해서 설명한다.

Visual과 inertial factor는 front-end에서 쓰인 VINS-mono에서 이미 설명이 되었으므로 여기에서는 자세한 설명 없이 넘어간다!

A. MAP Estimation

Optimum system state를 주어진 모든 측정값을 고려하여 MAP(사후 확률을 최적화)하는 것으로 정의한다.

다음과 같은 가정을 한다면 MAP 추정 문제를 cost들의 합을 최소화하는 문제로 변형할 수 있다.

• 모든 측정값은 서로 독립이다.
• 각 측정값의 noise가 zero-mean 가우시안분포를 따른다.

$\mathbf{\text{z}}$는 n개의 독립적인 센서 측정값의 집합

$r_p,H_p$는 시스템 state의 prior information(사전정보)를 내포

$r(\cdot )$은 각 측정값의 residual function

${\Vert \cdot \Vert }_P$는 마할라노비스 거리

 

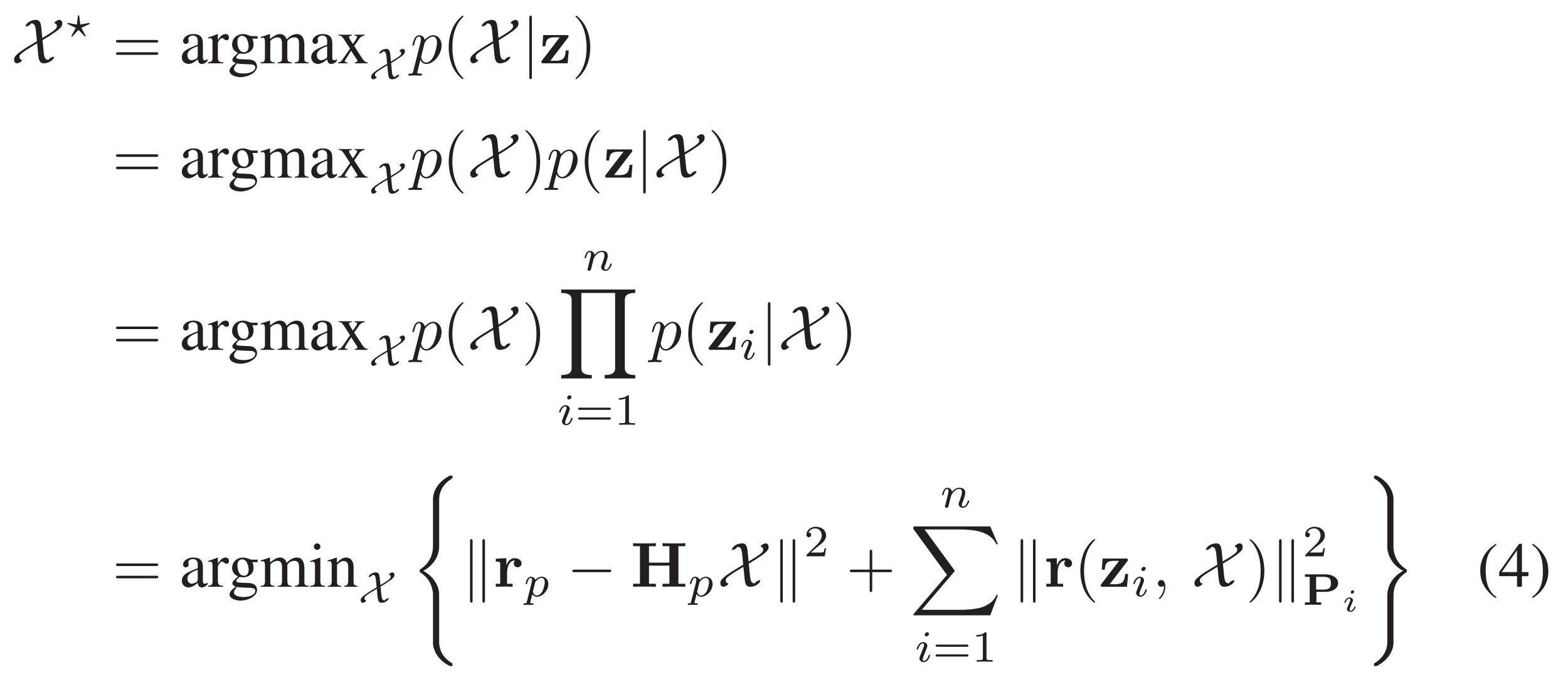
앞서 말했듯이 GVINS에서는 optimization problem을 state와 measurements와 관련된 각각의 factor로 문제를 구성한다.

아래 fig 6. 를 보면 factor graph가 어떻게 구성되어 있는지 알 수 있다.

fig 6

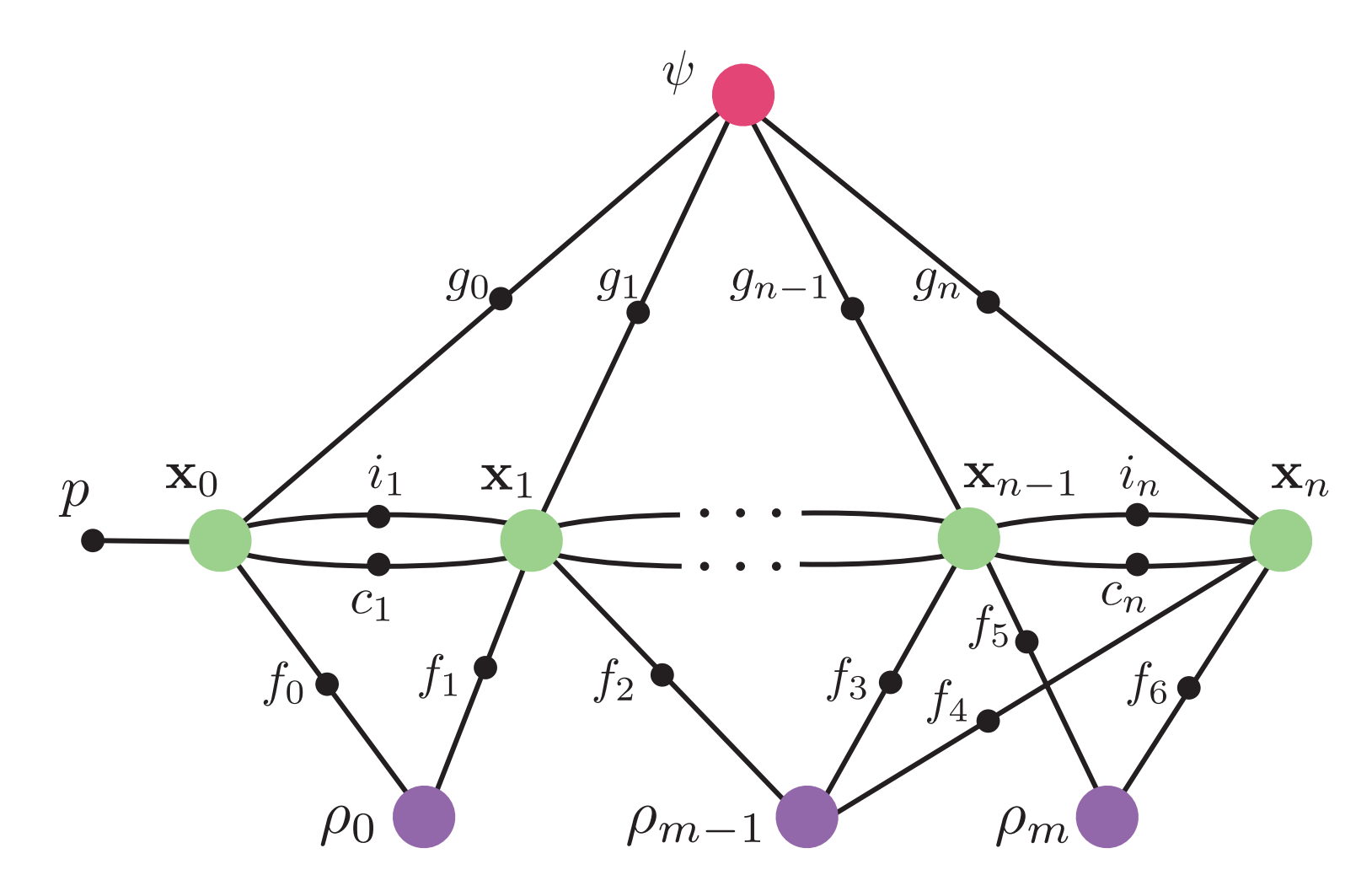
• large colored circles : system states
• small black circles : factors
• $i$ : inertial factor
• $f$ : visual factor
• $g$ : code pseudorange and Doppler factor
• $c$ : clock factor
• $p$ : prior factor(local world 프레임에서의 첫 번째 포즈를 제약하는 데 사용)

B. Inertial Factor

Inertial factor는 preintegration된 IMU의 measurement의 잔차를 이용한다.

Preintegration에 대한 설명은 ALIDA님의 VINS-mono 포스팅에 정말 자세히 설명되어 있다.

 

구성된 residual은 다음과 같다.

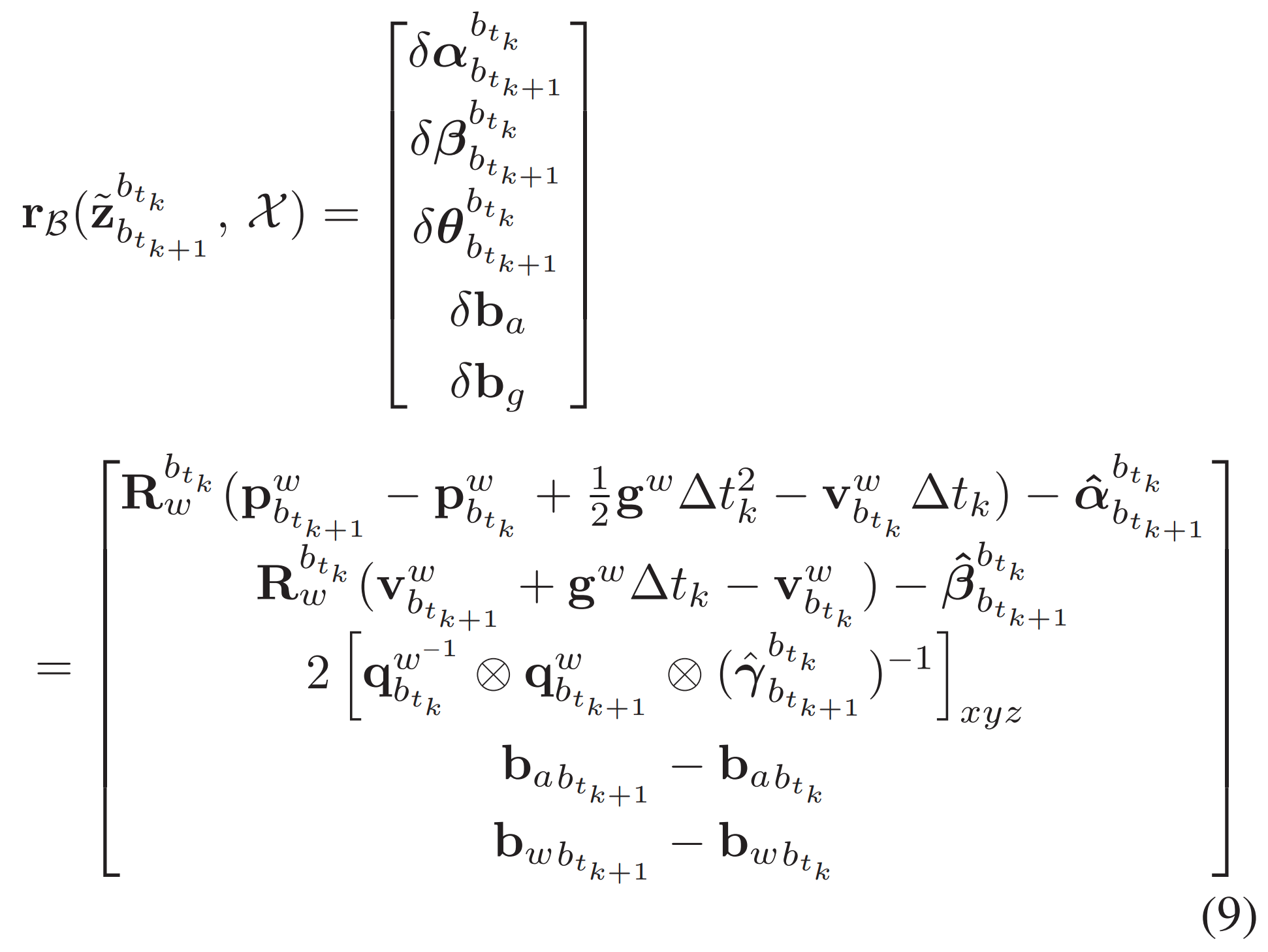
Residual에 포함된 상태 변수는 계속해서 최적화된다.

C. Visual Factor

역시나 VINS-mono에서 나온 내용이므로 간단하게 흐름만 짚고 넘어간다.

Image에서 Shi-Tomasi 코너 검출을 이용하여 sparse한 feature를 뽑고 iterative Lucas-Kanade 방법으로 추적한다.

Distortion 보정을 마친 feature points의 projection 과정은 다음과 같이 모델링 된다.

${\mathbf{x}}^{\mathbf{w}}$는 local world에 있는 3D 랜드마크다.

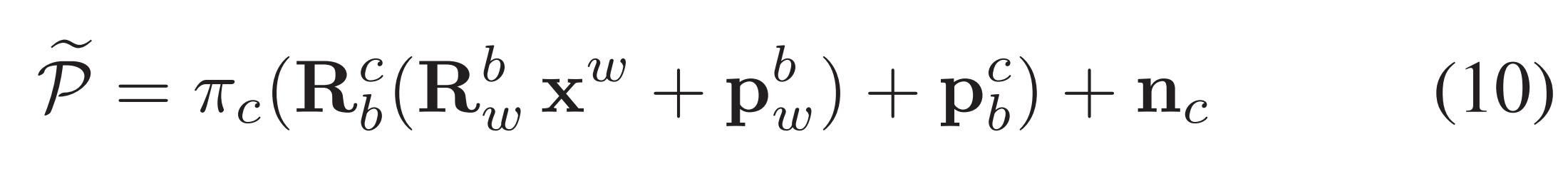
이 랜드마크를 image plane으로 투영하는 과정을 나타낸 식이다.

$\hat{p}$는 $[u,v{]}^T$이다.

Notation에 주의하여 rotation과 translation을 따라가면 직관적으로 이해된다.

$n_c$는 measurement noise이다.

 

자 이제 residual을 정의해본다.

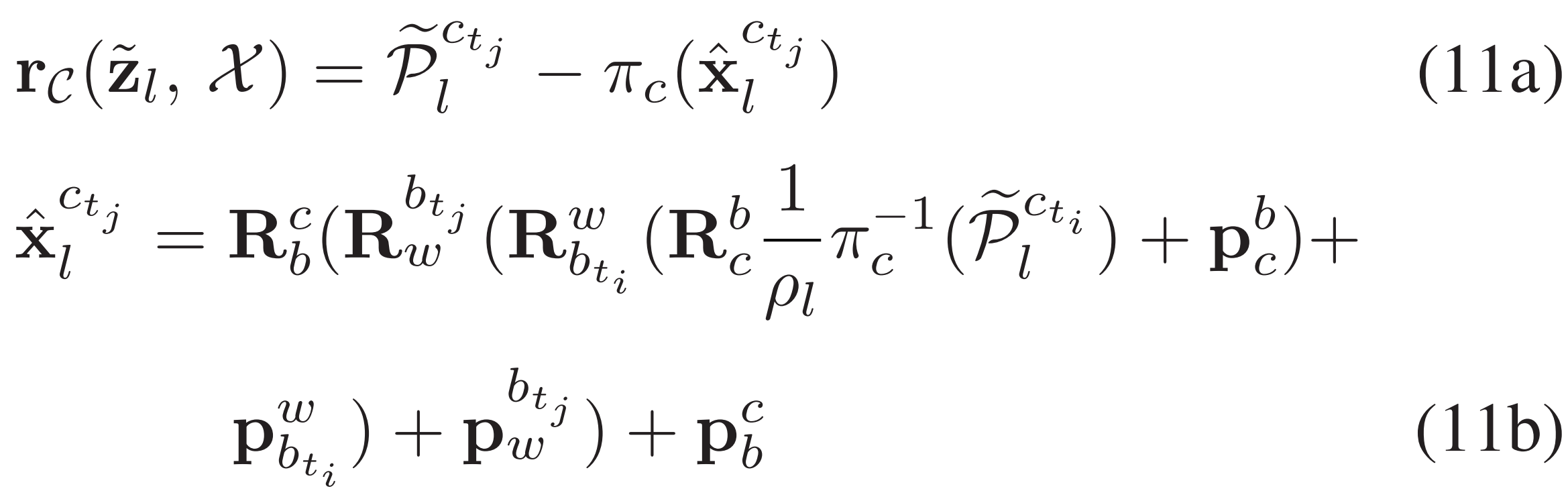
간단히 풀어서 설명하면..

Frame $i$에서 관찰된 Inverse depth ${\rho }_l$을 가진 어떤 feature $l$이 frame $j$에서 다시 발견되었을 경우 두 개의 frame간의 residual이다.

D. Code Pseudorange Factor

길고 긴 용어들이 나오는데, 그냥 번역하면 이상해져서 원문 그대로 해석했다.

 

GVINS에서 code pseudorange noise인 ${ϵ}_r^s$는 zero-mean Gaussian 분포로 가정한다.
분포는 이렇게 표현되며 $ϵ\sim N(0,{\sigma }_{r,pr}^s)$분산은 아래와 같이 정의된다.
$${\sigma }_{r,pr}^s=\frac{n_s\times n_{pr}}{si{n}^2{\theta }_{el}}$$

$n_s$는 broadcast satellite space accuracy index 이다. 
$n_{pr}$은 수신기에 의해 얻은 code pseudorange measurement 노이즈 인덱스이다.
${\theta }_{el}$은 수신기의 입장에서 봤을 때 위성의 고도를 나타낸다.

위성의 고도를 사용하는 이유는 두가지가 있는데 논문에 자세히 나와있다.
간단하게 말해서 불필요한 노이즈를 억제해줄 수 있기때문.

ECEF와 수신기의 local world 좌표계의 관계는 다음과 같이 정의된다.
$$p_r^e=R_n^e{R}_w^n(p_r^w-p_{anc}^w)+p_{anc}^e$$
$R_w^n$는 ENU와 local 좌표계 사이의 회전을 나타낸다.

ENU 좌표계의 upside와 local 좌표계의 z방향이 일치하여 회전만 달라지기 때문에 1자유도 회전이다.
이 회전은 yaw offset인 $\psi$로 표현된다.

GVINS에서 anchor point는 local frame의 원점에 지정한다.
Local world frame은 Fig. 2에 나타난 것 처럼 ENU frame의 시작점과 일치한다.
그래서 $p_{anc}^w$는 local world frame에서 anchor point의 좌표는 영벡터가 된다.

Local world frame에서 수신기의 위치는 아래의 state를 연관지을 수 있다.
$$p_r^w=p_b^w+R_b^w{p}_r^b$$
$b$는 base로 생각하면 local world에서 수신기의 위치를 쉽게 이해가능하다.
GNSS 측정값은 수신기에 의해 시간기록되기 때문에 ECI frame을 정의하여 신호를 수신할 때 ECEF frame 과 일치시킨다. 
그렇게 하면 신호가 수신기에 도달할 때 $p_r^E=p_r^e$이 된다.

지구 자전 때문에 신호가 위성에서 떠나 수신기에 도달할 때 ECEF frame에서 위치가 변하게 된다.
그래서 위성의 위치는 ECI frame으로 변환되어야 한다.
변환은 다음과 같이 표현된다.
$$p_s^E=R_z(-w_E{t}_f)p_s^{e^{{}^{\prime }}}$$
$R_z(\theta )$는 ECI frame의 $z$-axis에 대한 회전량이며 $t_f$는 GNSS 신호의 ToF이다.

마지막으로, $t_k$ 시간에 측정된 code pseudorange의 residual은 다음과 같이 구성될 수 있다.
이는 시스템 state인 {$p_{b_{t_k}}^w,q_{b_{t_k}}^w,\delta t_k,\psi$}와 위성 $s_j$와 연결되어있다.

따라서 다음과 같이 residual이 공식화 된다.

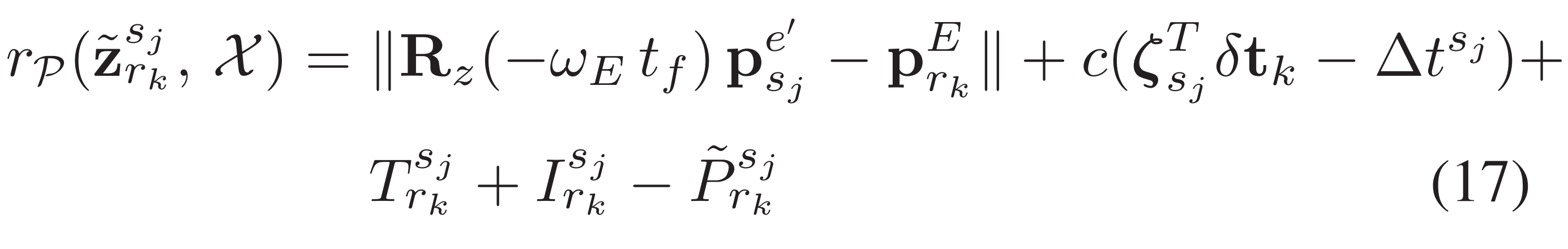
여기에서 $r_k$는 시간 $t_k$에서의 GNSS 수신기를 나타낸다.

E. Doppler Factor